IEA EBC Annex 60 EBC logo

Annex60.Utilities.Math.Functions.Examples

Collection of models that illustrate model use and test models

Information

This package contains examples for the use of models that can be found in Annex60.Utilities.Math.Functions.

Extends from Modelica.Icons.ExamplesPackage (Icon for packages containing runnable examples).

Package Content

Name Description
Annex60.Utilities.Math.Functions.Examples.CubicHermite CubicHermite Test problem for cubic hermite splines
Annex60.Utilities.Math.Functions.Examples.InverseXDerivativeCheck InverseXDerivativeCheck Model that checks the correct implementation of the 1st order derivative of InverseXRegularized
Annex60.Utilities.Math.Functions.Examples.InverseXDerivative_2_Check InverseXDerivative_2_Check Model that checks the correct implementation of the 2nd order derivative of InverseXRegularized
Annex60.Utilities.Math.Functions.Examples.InverseXRegularized InverseXRegularized Test problem for function that replaces 1/x around the origin by a twice continuously differentiable function
Annex60.Utilities.Math.Functions.Examples.IsMonotonic IsMonotonic Tests the correct implementation of the function isMonotonic
Annex60.Utilities.Math.Functions.Examples.Polynomial Polynomial  
Annex60.Utilities.Math.Functions.Examples.PowerLinearized PowerLinearized Test problem for function that linearizes y=x^n below some threshold
Annex60.Utilities.Math.Functions.Examples.RegNonZeroPower RegNonZeroPower  
Annex60.Utilities.Math.Functions.Examples.RegNonZeroPowerDerivativeCheck RegNonZeroPowerDerivativeCheck  
Annex60.Utilities.Math.Functions.Examples.RegNonZeroPowerDerivative_2_Check RegNonZeroPowerDerivative_2_Check  
Annex60.Utilities.Math.Functions.Examples.RegStep RegStep Example for inlined regStep function
Annex60.Utilities.Math.Functions.Examples.SmoothExponentialDerivativeCheck SmoothExponentialDerivativeCheck  
Annex60.Utilities.Math.Functions.Examples.SpliceFunction SpliceFunction  
Annex60.Utilities.Math.Functions.Examples.SpliceFunctionDerivativeCheck SpliceFunctionDerivativeCheck  
Annex60.Utilities.Math.Functions.Examples.TrapezoidalIntegration TrapezoidalIntegration Tests the correct implementation of the function trapezoidalIntegration

Annex60.Utilities.Math.Functions.Examples.CubicHermite Annex60.Utilities.Math.Functions.Examples.CubicHermite

Test problem for cubic hermite splines

Information

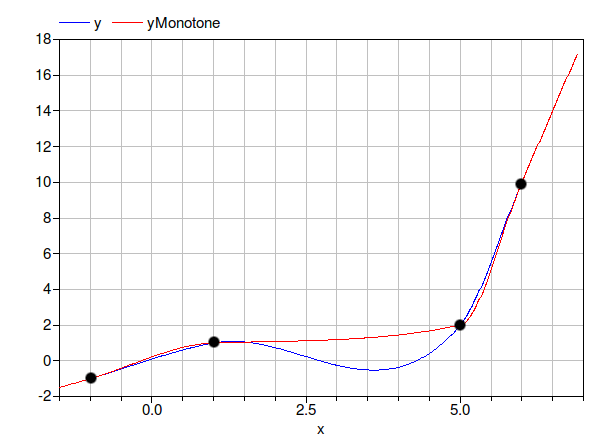
This example demonstrates the use of the function for cubic hermite interpolation and linear extrapolation. The example use interpolation with two different settings: One settings produces a monotone cubic hermite, whereas the other setting does not enforce monotonicity. The resulting plot should look as shown below, where for better visibility, the support points have been marked with black dots. Notice that the red curve is monotone increasing.

image

Extends from Modelica.Icons.Example (Icon for runnable examples).

Parameters

TypeNameDefaultDescription
Realxd[:]{-1,1,5,6}Support points
Realyd[size(xd, 1)]{-1,1,2,10}Support points
Reald[size(xd, 1)] Derivatives at the support points
RealdMonotone[size(xd, 1)] Derivatives at the support points
BooleanensureMonotonicitytrue 

Modelica definition

model CubicHermite "Test problem for cubic hermite splines" extends Modelica.Icons.Example; parameter Real[:] xd={-1,1,5,6} "Support points"; parameter Real[size(xd, 1)] yd={-1,1,2,10} "Support points"; parameter Real[size(xd, 1)] d(each fixed=false) "Derivatives at the support points"; parameter Real[size(xd, 1)] dMonotone(each fixed=false) "Derivatives at the support points"; parameter Boolean ensureMonotonicity=true; Real x "Independent variable"; Real y "Dependent variable without monotone interpolation"; Real yMonotone "Dependent variable with monotone interpolation"; Integer i "Integer to select data interval"; initial algorithm // Get the derivative values at the support points d := Annex60.Utilities.Math.Functions.splineDerivatives( x=xd, y=yd, ensureMonotonicity=false); dMonotone := Annex60.Utilities.Math.Functions.splineDerivatives(x=xd, y=yd, ensureMonotonicity=true); algorithm x := xd[1] + time*1.2*(xd[size(xd, 1)] - xd[1]) - 0.5; // i is a counter that is used to pick the derivative of d or dMonotonic // that correspond to the interval that contains x i := 1; for j in 1:size(xd, 1) - 1 loop if x > xd[j] then i := j; end if; end for; // Extrapolate or interpolate the data y := Annex60.Utilities.Math.Functions.cubicHermiteLinearExtrapolation( x=x, x1=xd[i], x2=xd[i + 1], y1=yd[i], y2=yd[i + 1], y1d=d[i], y2d=d[i + 1]); yMonotone := Annex60.Utilities.Math.Functions.cubicHermiteLinearExtrapolation( x=x, x1=xd[i], x2=xd[i + 1], y1=yd[i], y2=yd[i + 1], y1d=dMonotone[i], y2d=dMonotone[i + 1]); end CubicHermite;

Annex60.Utilities.Math.Functions.Examples.InverseXDerivativeCheck Annex60.Utilities.Math.Functions.Examples.InverseXDerivativeCheck

Model that checks the correct implementation of the 1st order derivative of InverseXRegularized

Information

This model validates the implementation of Annex60.Utilities.Math.Functions.inverseXRegularized and its first order derivative Annex60.Utilities.Math.Functions.BaseClasses.der_smoothTransition. If the derivative implementation is wrong, the simulation will stop with an error.

Extends from Modelica.Icons.Example (Icon for runnable examples).

Parameters

TypeNameDefaultDescription
Realdelta0.7Smoothing coefficient

Modelica definition

model InverseXDerivativeCheck "Model that checks the correct implementation of the 1st order derivative of InverseXRegularized" extends Modelica.Icons.Example; constant Real gain = 4 "Gain for computing the mass flow rate"; parameter Real delta = 0.7 "Smoothing coefficient"; Real x "Independent variable"; Real y_comp "Comparison value"; Real y "Dependent variable"; Real err "Integration error"; initial equation y = y_comp; equation x = time^3*gain; y = Annex60.Utilities.Math.Functions.inverseXRegularized( x = x, delta = delta); der(y_comp) = Annex60.Utilities.Math.Functions.BaseClasses.der_inverseXRegularized(x=x,delta=delta,x_der=der(x)); err = y-y_comp; assert(abs(err) < 1E-3, "Error in implementation."); end InverseXDerivativeCheck;

Annex60.Utilities.Math.Functions.Examples.InverseXDerivative_2_Check Annex60.Utilities.Math.Functions.Examples.InverseXDerivative_2_Check

Model that checks the correct implementation of the 2nd order derivative of InverseXRegularized

Information

This model validates the implementation of Annex60.Utilities.Math.Functions.inverseXRegularized and its second order derivative Annex60.Utilities.Math.Functions.BaseClasses.der_2_smoothTransition. If the derivative implementation is wrong, the simulation will stop with an error.

Extends from Modelica.Icons.Example (Icon for runnable examples).

Parameters

TypeNameDefaultDescription
Realdelta0.7Smoothing coefficient

Modelica definition

model InverseXDerivative_2_Check "Model that checks the correct implementation of the 2nd order derivative of InverseXRegularized" extends Modelica.Icons.Example; constant Real gain = 4 "Gain for computing the mass flow rate"; parameter Real delta = 0.7 "Smoothing coefficient"; Real x "Independent variable"; Real y_comp "Comparison value"; Real y "Dependent variable"; Real der_y_comp "1st order derivative of comparison value"; Real der_y "1st order derivative of dependent variable"; Real err "Integration error"; Real der_err "Integration error"; initial equation y = y_comp; der_y = der_y_comp; equation x = time^3*gain; y = Annex60.Utilities.Math.Functions.inverseXRegularized( x = x, delta = delta); der_y = der(y); der_y_comp = der(y_comp); der(der_y) = der(der_y_comp); err = y-y_comp; der_err = der_y-der_y_comp; assert(abs(err) < 1E-3, "Error in implementation."); assert(abs(der_err) < 1E-3, "Error in implementation."); end InverseXDerivative_2_Check;

Annex60.Utilities.Math.Functions.Examples.InverseXRegularized Annex60.Utilities.Math.Functions.Examples.InverseXRegularized

Test problem for function that replaces 1/x around the origin by a twice continuously differentiable function

Information

This example tests the implementation of Annex60.Utilities.Math.Functions.inverseXRegularized.

Extends from Modelica.Icons.Example (Icon for runnable examples).

Parameters

TypeNameDefaultDescription
Realdelta0.5Small value for approximation

Modelica definition

model InverseXRegularized "Test problem for function that replaces 1/x around the origin by a twice continuously differentiable function" extends Modelica.Icons.Example; Real x "Independent variable"; parameter Real delta = 0.5 "Small value for approximation"; final parameter Real deltaInv = 1/delta "Inverse value of delta"; final parameter Real a = -15*deltaInv "Polynomial coefficient"; final parameter Real b = 119*deltaInv^2 "Polynomial coefficient"; final parameter Real c = -361*deltaInv^3 "Polynomial coefficient"; final parameter Real d = 534*deltaInv^4 "Polynomial coefficient"; final parameter Real e = -380*deltaInv^5 "Polynomial coefficient"; final parameter Real f = 104*deltaInv^6 "Polynomial coefficient"; Real y "Function value"; Real xInv "Function value"; Real dy_dt "First derivative of y with respect to t"; Real d2y_dt2 "Second derivative of y with respect to t"; equation x=2*time-1; xInv = if ( abs(x) > 0.1) then 1 / x else 0; y = Annex60.Utilities.Math.Functions.inverseXRegularized( x=x, delta=delta, deltaInv=deltaInv, a=a, b=b, c=c, d=d, e=e, f=f); dy_dt=der(y); d2y_dt2=der(dy_dt); end InverseXRegularized;

Annex60.Utilities.Math.Functions.Examples.IsMonotonic Annex60.Utilities.Math.Functions.Examples.IsMonotonic

Tests the correct implementation of the function isMonotonic

Information

This example tests the correct implementation of the function Annex60.Utilities.Math.Functions.isMonotonic. If the function is implemented incorrect, the example will stop with an error.

Extends from Modelica.Icons.Example (Icon for runnable examples).

Modelica definition

model IsMonotonic "Tests the correct implementation of the function isMonotonic" extends Modelica.Icons.Example; Real x_incStrict[3] = {0, 1, 2} "strictly increasing"; Real x_notMon[3] = {0, 3, 2} "not monotonic"; Real x_incWeak[4] = {0, 1, 1, 2} "weakly increasing"; Real x_notWeak[4] = {0, 3, 3, 2} "not weakly monotonic"; Real x_decStrict[3] = {2.5, 2, 0.1} "strictly decreasing"; Real x_decWeak[4] = {3, 1, 1, 0.5} "weakly decreasing"; equation // Tests with weak monotonicity //strictly increasing assert(Annex60.Utilities.Math.Functions.isMonotonic(x_incStrict, strict=false), "Error. Function should have returned true."); //not monotonic assert(false == Annex60.Utilities.Math.Functions.isMonotonic(x_notMon, strict=false), "Error. Function should have returned true."); //weakly increasing assert(Annex60.Utilities.Math.Functions.isMonotonic(x_incWeak, strict=false), "Error. Function should have returned true."); //not weakly monotonic assert(false == Annex60.Utilities.Math.Functions.isMonotonic(x_notWeak, strict=false), "Error. Function should have returned true."); //strictly decreasing assert(Annex60.Utilities.Math.Functions.isMonotonic({2.5, 2, 0.1}, strict=false), "Error. Function should have returned true."); //weakly decreasing assert(Annex60.Utilities.Math.Functions.isMonotonic({3, 1, 1, 0.5}, strict=false), "Error. Function should have returned true."); // Tests with strict monotonicity //strictly increasing assert(Annex60.Utilities.Math.Functions.isMonotonic(x_incStrict, strict=true), "Error. Function should have returned true."); //not monotonic assert(false == Annex60.Utilities.Math.Functions.isMonotonic(x_notMon, strict=true), "Error. Function should have returned true."); //weakly increasing assert(false == Annex60.Utilities.Math.Functions.isMonotonic(x_incWeak, strict=true), "Error. Function should have returned true."); //not weakly monotonic assert(false == Annex60.Utilities.Math.Functions.isMonotonic(x_notWeak, strict=true), "Error. Function should have returned true."); //strictly decreasing assert(Annex60.Utilities.Math.Functions.isMonotonic(x_decStrict, strict=true), "Error. Function should have returned true."); //weakly decreasing assert(false == Annex60.Utilities.Math.Functions.isMonotonic(x_decWeak, strict=true), "Error. Function should have returned true."); end IsMonotonic;

Annex60.Utilities.Math.Functions.Examples.Polynomial Annex60.Utilities.Math.Functions.Examples.Polynomial

Information

This example verifies the correct implementation of Annex60.Utilities.Math.Functions.polynomial.

Extends from Modelica.Icons.Example (Icon for runnable examples).

Modelica definition

model Polynomial extends Modelica.Icons.Example; Real x "Function value"; equation x=Annex60.Utilities.Math.Functions.polynomial(x=time^3-2, a={2, 4, -4, 5}); end Polynomial;

Annex60.Utilities.Math.Functions.Examples.PowerLinearized Annex60.Utilities.Math.Functions.Examples.PowerLinearized

Test problem for function that linearizes y=x^n below some threshold

Information

This example tests the implementation of Annex60.Utilities.Math.Functions.powerLinearized.

Extends from Modelica.Icons.Example (Icon for runnable examples).

Modelica definition

model PowerLinearized "Test problem for function that linearizes y=x^n below some threshold" extends Modelica.Icons.Example; Real T4(start=300^4) "Temperature raised to 4-th power"; Real T "Temperature"; Real TExact "Temperature"; equation T = (1+500*time); T = Annex60.Utilities.Math.Functions.powerLinearized(x=T4, x0=243.15^4, n=0.25); TExact = abs(T4)^(1/4); end PowerLinearized;

Annex60.Utilities.Math.Functions.Examples.RegNonZeroPower Annex60.Utilities.Math.Functions.Examples.RegNonZeroPower

Information

This example tests the implementation of Annex60.Utilities.Math.Functions.regNonZeroPower.

Extends from Modelica.Icons.Example (Icon for runnable examples).

Modelica definition

model RegNonZeroPower extends Modelica.Icons.Example; Real y "Function value"; equation y=Annex60.Utilities.Math.Functions.regNonZeroPower( time, 0.3, 0.5); end RegNonZeroPower;

Annex60.Utilities.Math.Functions.Examples.RegNonZeroPowerDerivativeCheck Annex60.Utilities.Math.Functions.Examples.RegNonZeroPowerDerivativeCheck

Information

This example checks whether the function derivative is implemented correctly. If the derivative implementation is not correct, the model will stop with an assert statement.

Extends from Modelica.Icons.Example (Icon for runnable examples).

Parameters

TypeNameDefaultDescription
Realn0.33Exponent
Realdelta0.1Abscissa value where transition occurs

Modelica definition

model RegNonZeroPowerDerivativeCheck extends Modelica.Icons.Example; parameter Real n=0.33 "Exponent"; parameter Real delta = 0.1 "Abscissa value where transition occurs"; Real x; Real y; initial equation y=x; equation x=Annex60.Utilities.Math.Functions.regNonZeroPower( time^3,n, delta); der(y)=der(x); assert(abs(x-y) < 1E-2, "Model has an error"); end RegNonZeroPowerDerivativeCheck;

Annex60.Utilities.Math.Functions.Examples.RegNonZeroPowerDerivative_2_Check Annex60.Utilities.Math.Functions.Examples.RegNonZeroPowerDerivative_2_Check

Information

This example checks whether the function derivative is implemented correctly. If the derivative implementation is not correct, the model will stop with an assert statement.

Extends from Modelica.Icons.Example (Icon for runnable examples).

Parameters

TypeNameDefaultDescription
Realn0.33Exponent
Realdelta0.7Smoothing coefficient

Modelica definition

model RegNonZeroPowerDerivative_2_Check extends Modelica.Icons.Example; parameter Real n=0.33 "Exponent"; constant Real gain = 4 "Gain for computing the mass flow rate"; parameter Real delta = 0.7 "Smoothing coefficient"; Real x "Independent variable"; Real y_comp "Comparison value"; Real y "Dependent variable"; Real der_y_comp "1st order derivative of comparison value"; Real der_y "1st order derivative of dependent variable"; Real err "Integration error"; Real der_err "Integration error"; initial equation y = y_comp; der_y = der_y_comp; equation x = time^3*gain; y = Annex60.Utilities.Math.Functions.regNonZeroPower( x = x, n = n, delta = delta); der_y = der(y); der_y_comp = der(y_comp); der(der_y) = der(der_y_comp); err = y-y_comp; der_err = der_y-der_y_comp; assert(abs(err) < 1E-3, "Error in implementation."); assert(abs(der_err) < 1E-3, "Error in implementation."); end RegNonZeroPowerDerivative_2_Check;

Annex60.Utilities.Math.Functions.Examples.RegStep Annex60.Utilities.Math.Functions.Examples.RegStep

Example for inlined regStep function

Information

This example tests the implementation of Annex60.Utilities.Math.Functions.regStep.

Extends from Modelica.Icons.Example (Icon for runnable examples).

Modelica definition

model RegStep "Example for inlined regStep function" extends Modelica.Icons.Example; Real y "Function value"; equation y=Annex60.Utilities.Math.Functions.regStep(time, 1, -1, 1e-5); end RegStep;

Annex60.Utilities.Math.Functions.Examples.SmoothExponentialDerivativeCheck Annex60.Utilities.Math.Functions.Examples.SmoothExponentialDerivativeCheck

Information

This example checks whether the function derivative is implemented correctly. If the derivative implementation is not correct, the model will stop with an assert statement.

Extends from Modelica.Icons.Example (Icon for runnable examples).

Parameters

TypeNameDefaultDescription
Realdelta0.5Smoothing area

Modelica definition

model SmoothExponentialDerivativeCheck extends Modelica.Icons.Example; parameter Real delta = 0.5 "Smoothing area"; Real x "Independent variable"; Real y "Approximate function value"; Real y_comp "Approximate function value"; Real ex "Exact function value"; Real err "Error"; initial equation y=y_comp; equation x = time^3; y_comp=Annex60.Utilities.Math.Functions.smoothExponential( x=x, delta=delta); der(y)=der(y_comp); err = y_comp-y; assert(abs(err) < 1E-2, "Model has an error"); ex=exp(-abs(x)); end SmoothExponentialDerivativeCheck;

Annex60.Utilities.Math.Functions.Examples.SpliceFunction Annex60.Utilities.Math.Functions.Examples.SpliceFunction

Information

This example checks whether the function derivative is implemented correctly. If the derivative implementation is not correct, the model will stop with an assert statement.

Extends from Modelica.Icons.Example (Icon for runnable examples).

Modelica definition

model SpliceFunction extends Modelica.Icons.Example; Real y "Function value"; equation y=Annex60.Utilities.Math.Functions.spliceFunction( pos=10, neg=-10, x=time-0.4, deltax=0.2); end SpliceFunction;

Annex60.Utilities.Math.Functions.Examples.SpliceFunctionDerivativeCheck Annex60.Utilities.Math.Functions.Examples.SpliceFunctionDerivativeCheck

Information

This example checks whether the function derivative is implemented correctly. If the derivative implementation is not correct, the model will stop with an assert statement.

Extends from Modelica.Icons.Example (Icon for runnable examples).

Parameters

TypeNameDefaultDescription
Realdelta0.2Smoothing area

Modelica definition

model SpliceFunctionDerivativeCheck extends Modelica.Icons.Example; parameter Real delta = 0.2 "Smoothing area"; Real deltax "Smoothing area as a function of x"; Real x "Independent variable"; Real y "Approximate function value"; Real y_comp "Approximate function value"; Real err "Error"; initial equation y=y_comp; equation x = time^3; deltax=delta*10*time^8+0.1; // Because the derivative is implemented for all arguments, // we make pos, neg and deltax also functions of time y=Annex60.Utilities.Math.Functions.spliceFunction( pos=10*x^3, neg=-10*x^2, x=x, deltax=deltax); der(y)=der(y_comp); err = y-y_comp; assert(abs(err) < 1E-2, "Model has an error"); end SpliceFunctionDerivativeCheck;

Annex60.Utilities.Math.Functions.Examples.TrapezoidalIntegration Annex60.Utilities.Math.Functions.Examples.TrapezoidalIntegration

Tests the correct implementation of the function trapezoidalIntegration

Information

Tests the correct implementation of function Annex60.Utilities.Math.Functions.trapezoidalIntegration.

Integrands y1[7]={72, 70, 64, 54, 40, 22, 0} are the function values of y = -2*x^2-72 for x = {0,1,2,3,4,5,6}. The trapezoidal integration over the 7 integrand points should give a result of 286.

Extends from Modelica.Icons.Example (Icon for runnable examples).

Modelica definition

model TrapezoidalIntegration "Tests the correct implementation of the function trapezoidalIntegration" extends Modelica.Icons.Example; Real y1[7] = {72, 70, 64, 54, 40, 22, 0}; //function values of y = -2*x^2-72 for x={0,1,2,3,4,5,6} Real y "Integration result"; //Real y2[7] = {0.3333, 1.0, 3.0, 9.9, 27.0, 81.0, 243.0}; // //function values of y = 3^(3x-1) for x=0:0.3333:2 algorithm y := Annex60.Utilities.Math.Functions.trapezoidalIntegration(N=7, f=y1, deltaX=1); assert(y - 286.0 < 1E-4, "Error. Function should have returned 286."); end TrapezoidalIntegration;
http://iea-annex60.org